-
Hey, guest user. Hope you're enjoying NeoGAF! Have you considered registering for an account? Come join us and add your take to the daily discourse.
The Math Help Thread
- Thread starter -COOLIO-
- Start date
- Status
Double post cause again, I'm using a phone and don't know how to multiquote.cpp_is_king said:Someone already showed you one way of doing the first one, so I'll do the second one.
First of all, I assume you made a typo there. The first and second terms of the subtraction are actually identical, you just reversed the order of sin and cos. If you wrote it correctly the the answer is trivially 0. I assume it should have been:
sin(3theta)cos(2theta)-cos(3theta)sin(2theta)
Any time you see something like a*b +/- c*d where a, b, c, and d are some sort of sine or cosine you should immediately think of the addition / subtraction formulas:
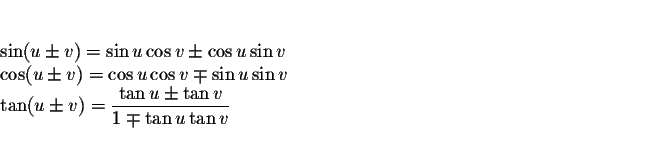
Is there any way to make either of these formulas work? The formula for sin(u-v) fits perfectly. You end up with:
u = 2theta
v = 3theta
and the answer is thus sin(2theta - 3theta) = sin(-theta) = -sin(theta)
Thanks! Hadn't actually looked into those yet, makes sense now. Time to learn how to derive those formulas
Edit: thx a bunch bigander.
Lagspike_exe
Member
One and a half cat eats one and a half mice in one and a half days. How many mices will be eaten in 20 days by 5 cats?
The best way to do this question is to make the measurement in base units, to give ourselves a rate we can understand. Let's reduce the first sentence, step by step.Lagspike_exe said:
If we go down to one cat, we're cutting production by 33%. So, one cat (still in one and a half days) could eat one mouse.
But, we have to bring it down even further: in only one day, we get another 33% reduction. So, in one day, one cat can eat 2/3rds of a mouse.
Moving to the last step, if we multiply 2/3rds by 5 cats, we get 10/3rds mice eaten in one day...
And in twenty days, we get 10/3 * 20 = 200/3 mice will be eaten in total.
Leona Lewis
Banned
Is anyone here really good at Game Theory? I'm taking an intro course in Game Theory and I need help with a Bayesian equilibrium problem my TA's too ill to help me with at the moment. Thanks!
cpp_is_king
Member
Leona Lewis said:
No guarantees, but post your question anyway.
Leona Lewis
Banned
Here's the question:
Suppose there are two countries that are making a simultaneous choice between accepting a peace deal that gives each a payoff of 1/2 and fighting a war, whose outcome is uncertain. If both countries accept then they get the settlement payoff, but any country can choose to start a war.
The outcome of a war is determined by the countries' types. Each country can be a weak, moderate, or strong type. In a war strong types beat weak and moderate ones, moderate ones beat weak ones, and weak ones always lose. When countries of the same strength meet, each wins with probability 1/2.
Also each country has private information, in particular they know their own strength but think that the opponent is equally likely to be weak, moderate, or strong. Finally, suppose the cost of war for all countries is c = 1/6 (c = cost), the strong type fights in equilibrium and the weak type does not in both countries. Does the moderate type of country fight or accept a settlement in equilibrium? Explain your answer.
I can answer questions if anyone needs clarification! I just don't know where to start with this one. So far game theory has been really fun (I've already mastered mixed strategy equilibria), but this new Bayesian equilibria just confuse me.
Suppose there are two countries that are making a simultaneous choice between accepting a peace deal that gives each a payoff of 1/2 and fighting a war, whose outcome is uncertain. If both countries accept then they get the settlement payoff, but any country can choose to start a war.
The outcome of a war is determined by the countries' types. Each country can be a weak, moderate, or strong type. In a war strong types beat weak and moderate ones, moderate ones beat weak ones, and weak ones always lose. When countries of the same strength meet, each wins with probability 1/2.
Also each country has private information, in particular they know their own strength but think that the opponent is equally likely to be weak, moderate, or strong. Finally, suppose the cost of war for all countries is c = 1/6 (c = cost), the strong type fights in equilibrium and the weak type does not in both countries. Does the moderate type of country fight or accept a settlement in equilibrium? Explain your answer.
I can answer questions if anyone needs clarification! I just don't know where to start with this one. So far game theory has been really fun (I've already mastered mixed strategy equilibria), but this new Bayesian equilibria just confuse me.
Lagspike_exe
Member
Your answer is correct, thanks for help.Feep said:
Leona Lewis
Banned
I should also add that by "simultaneous choice," I mean that neither country knows what the other will choose. HALP!? :-(Leona Lewis said:
cpp_is_king
Member
KingK said:
Make a triangle and figure out the angle using the side lengths, and make sure the answer you give is in the range 0<=theta<=2pi when measured counter-clockwise from the positive x-axis.
close to the edge
Member
http://en.wikipedia.org/wiki/Complex_number#Polar_formKingK said:
Drawing works too but isn't as exact, depending on how well you can draw.
EDIT: Never mind I figured it all out, I am an idiot.
Holy shit, theres a GAF thread for everything.
I have to take this stupid online SAT prep class, and I'm terrible at math since I haven't taken it in a semester, and math is my worst subject. I am in dire need of assistance, gentlemen.
Feel free to laugh at my stupidity, I will laugh with you:
I said C, but it said it was incorrect. I don't even know...
Yeah....
JackEtc said:
If you got the answer but in case you want to know why it's the answer...
For the first question, you can set up a word problem.
Let x be your original price.
original price + 5% sales tax of original price = final price
x + 0.05x = 14910
Adding the like terms together gets you:
1.05x = 14910
So 14910/1.05 = x, your original value, 14200
So 14910 - 14200 = the extra money you paid with the 5% sales tax, which is $710.
And for the second problem....
Volume of a cube is length x width x height. With a cube, all sides are the same length. So it's basically side x side x side.
side = 4.5x10^-2 which is 0.045
So 0.045 x 0.045 x 0.045 = 9.1125 x 10^-5 which is your volume
For the first question it should be something like this though I'm not fully sure
He has 30 years. And his ratio is 7/3. Think of it as 70% and 30%. So 70% of the 30 years is years he taught. While 30% of 30 is years he has left to retirement.
So 0.3 * 30 = 9 years until retirement
0.7 * 30 = 21 years taught
So the answer should be 9. To check just do 21/9 and you will get 7/3
As for the second question I think it's just
(12 + x) / 2 = 15 where x is the other speed he needs to run for the second half
12 + x = 30
x = 18
He has 30 years. And his ratio is 7/3. Think of it as 70% and 30%. So 70% of the 30 years is years he taught. While 30% of 30 is years he has left to retirement.
So 0.3 * 30 = 9 years until retirement
0.7 * 30 = 21 years taught
So the answer should be 9. To check just do 21/9 and you will get 7/3
As for the second question I think it's just
(12 + x) / 2 = 15 where x is the other speed he needs to run for the second half
12 + x = 30
x = 18
The first one is 9 since you've already worked 7 years for every 3 of the total 30 years.
Think of it this way: (7 + 3) +(7 + 3) + (7 + 3) = 30, you haven't worked the "3s" yet and 3*3=9.
Second one:
You ran 1/2 a race at 12 mph and want to finish at an average of 15 mph. So we have to find what other number plus 12 averages to 15. Mathematically, (12+x)/2=15, x = 18.
Think of it this way: (7 + 3) +(7 + 3) + (7 + 3) = 30, you haven't worked the "3s" yet and 3*3=9.
Second one:
You ran 1/2 a race at 12 mph and want to finish at an average of 15 mph. So we have to find what other number plus 12 averages to 15. Mathematically, (12+x)/2=15, x = 18.
JackEtc said:
This question is confusing me, so someone else might be able to help. I think it might be the wording.
JackEtc said:
Average is the (first number) + (second number) divided by 2.
In other words, ((12km/h) + x)/2 = 15km/h
So the 10km distance of the race is unnecessary information. We're not interested in distance, just the average of the two speeds = 15km/hr.
so if (12 + x)/2 = 15
12 + x = 30
x = 18 km/h
JackEtc said:
10/4b = q/10b
Normally, for problems like these, we'd use substitution. Since we have two variables that we don't know, we can solve for one to equal the other, and the "substitute" it in, and find the other.
But if you cross multiply.
100b = 4bq
100b/4b = q
You'll find that the b on the top conveniently cancels out with the b on the bottom
leaving you with 100/4 = q
q = 25
cpp_is_king
Member
The Lamp said:
Just be very careful about breaking down the problem, take it line by line
This doesn't mean he needs 30 MORE years, just that he needs 30 years total.
So,
Years Taught = X
Years Remaining to Retirement = 30 - X
X / (30 - X) = 7 / 3
3X = 7(30 - X)
3X = 210 - 7X
10X = 210
X = 21
We have X, but we need 30 - X. Thus the answer is 9
D
JackEtc said:
18 seems like such a logical and simple answer. However, I calculated it differently and ended up at 20.
for 10 km at an avg speed of 15 km/h it should take 10/15 h = 2/3 h
the first 5 km at 12 km/h take 5/12 h
goal time is 2/3 h, so 8/12 h. so the second part should take 3/12 h.
5 km / (3/12 h) = 60/3 km/h = 20 km/h
-----
it's easy to confuse the two approaches here.
if you first drive 30 minutes a 12 km/h and then 30 minutes at 18 km/h your average speed will be 15 km/h. but if you drive at each speed for 5 km the second part doesn't take as long.
cpp_is_king
Member
The Lamp said:
This is not correct. You can't average "speed" this way because it is a continuous quantity. Average speed is defined as (total distance travelled) / (time it took to get there). Makes sense if you think about it, if you go 30 miles and it took half an hour, then you were going about 60 miles / hour. That's average speed.
The first half is 5km long, and since he was going 12km/hr it took him 5/12 hr to make it.
The second half is also 5km, and he will travel x km/hr to get there. So it will take him 5/x hr to make it. The total distance is 10 km, so for the average speed to be 15km/hr, the total time travelled should be 10/15 hours, or 2/3 hours.
Thus, we have
5/12 + 5/x = 2/3
5x/12x + 60/12x = 8/12
(5x + 60) = 8x
3x = 60
x = 20
ThanksVision
Member
I've got a few conic equations in standard form, but I need to solve them for y to put them in my calculator, but I'm having trouble.
circle
(x-33/2)^2 + (y-3/2)^2 = 1/4
ellipse
(x-17)^2 + ((y+20)^2)/1 = 1
4
I know how to graph these manually, but my teacher wants to print them so I have to use the calculator. Whenever I plug in my answer it never graphs though...
circle
(x-33/2)^2 + (y-3/2)^2 = 1/4
ellipse
(x-17)^2 + ((y+20)^2)/1 = 1
4
I know how to graph these manually, but my teacher wants to print them so I have to use the calculator. Whenever I plug in my answer it never graphs though...
The joint density of Y1, the proportion of the capacity of the tank that is stocked at the beginning of the week, and Y2, the proportion of the capacity sold during the week is given by f( y1,y2) = { 3y1, 0< y2 < y1 <= 1 }
Find F(1/2, 1/3) = P(Y1 <= 1/2, Y2 <= 1/3)?
I integrate 3y1dy2dy1 from 0 to 1/3 then 0 to 1/2 to get .125, however the books says .1065 is the correct answer. I haven't taken a multivariate calc class so I'm still a little confused by double integration.
Find F(1/2, 1/3) = P(Y1 <= 1/2, Y2 <= 1/3)?
I integrate 3y1dy2dy1 from 0 to 1/3 then 0 to 1/2 to get .125, however the books says .1065 is the correct answer. I haven't taken a multivariate calc class so I'm still a little confused by double integration.
cpp_is_king
Member
Ace 8095 said:
integrating from 0 to 1/3 on y2 violates the first inequality -- that 0< y2 < y1. Break it into two integrals. [0<y1<1/3, 0<y2<y1] and [1/3<y1<1/2, 0<y2<1/3]
cpp_is_king
Member
Ace 8095 said:
Sure, I'll try to explain. This problem is a little tricky.
Suppose we were told to perform a similar calculation, but this time in 2D, so just one variable. Let's say we had to solve the following:
Calculate the area under the graph y = 3x from 0 to 1, subject to the constraint 0 < y < 1. Draw this out on a piece of paper and you end up with something like the following, where the shaded green area is the area you need to compute.
We can calculate the area using basic geometry of a trapezoid, but we can also do it by treating it as 2 separate integrals. The first integral is from x=0 to x=1/3 of the line y=3x. The second integral is from x=1/3 to x=1 of the line y=1. If you correlate these two integrals to the graph you've drawn, you will notice that they cover the entire area of the shaded region. Since integral is just area represented, you know this must work.
So now how to apply this to your case? It's hard to draw on a sheet of paper since it's in 3D but the concept is the same. The first inequality tells you that 0 < y2 < y1. The other tells you that y2 < 1/3 and y1 < 1/2.
If you were to just integrate this normally (as you originally did), there would be two problems:
First, y2 would be bounded only by the number 1/3. In the 2D world, this is like taking the area of a rectangle. When you're doing multiple integrations like this, ALL possible combinations of the 2 ranges become valid. So if you have a double integral over the range [0,1/2] [0,1/3] then every possible pair of numbers in those 2 ranges are factored into the result. 0,0 is one possibility, so is 1/2,1/3, and 0,1/3, and 1/2,0, and everything else. What you need is a way to say "as I am integrating over the first range, limit the the second range to whatever number is currently the value of the function in the first range. It seems confusing in words but it's easier to visualize.
The second problem is that, if you were to just solve the first problem described above, you would still not be integrating over the correct range. If your only condition is that 0<y2<y1 then since y1 goes up to 1/2 you would be letting y2 run all the way up to 1/2 once you get near the end of the y1 interval. But we only want y2 going up to 1/3. The way to solve this is by breaking it into a separate interval. Just like in the 2D example I gave originally, there are 2 different conditions.
1) As long as y1 <= 1/3, then we can integrate directly over the range 0<y2<y1, there will never be a problem. All the inequalities will be satisfied. But as soon as y1 goes over 1/3, we'll have a problem because then so will y2. So we need to stop the first integral at y1=1/3
2) That means we still haven't integrated anything in the range y1=1/3 to y1=1/2. The integral that says that 0<y2<y1 we don't even need to look at for this part of the integral, because it's ALWAYS true, since the smallest y1 can even be is 1/3, and the max that y2 can be is 1/3. So in this case we want to integrate y2 from 0 to 1/3.
This leads to the 2 integrals I gave originally.
cpp_is_king
Member
Ace 8095 said:
Also, I just thought of a neat way to visualize the concept of your limit of integration being a variable instead of a constant, and how this relates to double integrals. Every single time you do a single integral you are already doing a double integral with a variable limit of integration, you just don't realize it.
In the case of a single integral, what you're actually doing is saying "integrate this entire rectangular area, but where the limit of integration along the y-axis is this function I'm specifying". Well, integrating a rectangle is like integrating 1 dx, or some other constant.
Concrete example:
Suppose you have to integrate y = 3x from x=0 to x=5. What you are really doing is integrating from x=0 to x=5, and y=0 to y=3x of the function x=1.
So you can write this as a double integral:
S[0;5] S[0;3x] 1 dy dx
It's easy to see how this works. As soon as you solve the inner integral you just get
S[0;5] 3x dx
which is the original problem.
Anyway, the point of this is just to emphasize that variable-limits are nothing magic, you've been doing it all along.
Mind if I ask one more problem to check my intuition?
f(y1,y2) = 6(1-y1), 0<y2<y1<1
Find P(y2 < 3/4, y1 > 1/2)
Since this has two inequalities I will need to break it into two integrals. Since y1 is greater than y2, and y1 is greater than 1/2 I have S[0,1/2]S[1/2,1] 6(1-y1)dy1,dy2.
Since Since y2 is between 1/2 and 3/4 and y1 is between y2 and 1 I have S[1/2,3/4]S[y2,1] 6(1-y1)dy1,dy2.
Is this correct?
f(y1,y2) = 6(1-y1), 0<y2<y1<1
Find P(y2 < 3/4, y1 > 1/2)
Since this has two inequalities I will need to break it into two integrals. Since y1 is greater than y2, and y1 is greater than 1/2 I have S[0,1/2]S[1/2,1] 6(1-y1)dy1,dy2.
Since Since y2 is between 1/2 and 3/4 and y1 is between y2 and 1 I have S[1/2,3/4]S[y2,1] 6(1-y1)dy1,dy2.
Is this correct?
cpp_is_king
Member
This one is even trickier, and I think you might be wrong actually Is this a problem for which you can check the answer? The reason I think it's wrong is that your breakdown doesn't result in full coverage of the entirety of 0<y2<3/4 and 1/2<y1<1.
One good way to start these problems is to write every single limit on a single 1-dimensional number line and then analyze each of the "sections" of this number line independently independently. Maybe you'll find that points can be deleted from the number line if multiple regions share the same properties, but you might find you need all of them. In this case, you get a number line with 4 points. 0, 1/2, 3/4, and 1. y2 needs to be integrated over the first 2 intervals, and y1 over the last 2 intervlas. So there's a max of 4 different integrals we need to break this up into, although we might be able to get by with fewer. I say 4 because each variable needs to be considered over each interval.
It's important to remember that we need full coverage over both intervals at the same time. You might be tempted to look at this number line and say "well i don't have to worry about 0 to 1/2 because y1 isn't even integrated there". But what the double integration means is that for every value of y2 over the range of integration, we need to be integrating y1 from 1/2 to 1.
Thus, while y2 is being integrated from 0 to 1/2, we integrate y1 from 1/2 to 1. No problem, 0<y2<y1<1 is satisfied here.
From 1/2 to 3/4 we have a different story. This is where we need to use a variable range of integration. y2 should be integrated from 1/2 to 3/4, but y1 should be integrated from y1 to 3/4. Alternatively, you can swap the order of integration and integrate y1 from 1/2 to 3/4 and integrate y2 from 1/2 to y1. You can prove that this order of integration swap works analytically for the general case, but here you only need a conceptual understanding like "yea, i can see how either way means the same thing". So that gives your second double integral (Note that in the image below I used the "alternate" method so that the order is consistent across all the integrals. But try it the reverse way just to convince yourself it's the same.
For the range 3/4 to 1, just like in the first case the inequality is always true, so we don't need a variable range of integration. only 0<y2<3/4 and 3/4<y1<1.
So, in closing, you end with the following:
Is this a problem for which you can check the answer? The reason I think it's wrong is that your breakdown doesn't result in full coverage of the entirety of 0<y2<3/4 and 1/2<y1<1. One good way to start these problems is to write every single limit on a single 1-dimensional number line and then analyze each of the "sections" of this number line independently independently. Maybe you'll find that points can be deleted from the number line if multiple regions share the same properties, but you might find you need all of them. In this case, you get a number line with 4 points. 0, 1/2, 3/4, and 1. y2 needs to be integrated over the first 2 intervals, and y1 over the last 2 intervlas. So there's a max of 4 different integrals we need to break this up into, although we might be able to get by with fewer. I say 4 because each variable needs to be considered over each interval.
It's important to remember that we need full coverage over both intervals at the same time. You might be tempted to look at this number line and say "well i don't have to worry about 0 to 1/2 because y1 isn't even integrated there". But what the double integration means is that for every value of y2 over the range of integration, we need to be integrating y1 from 1/2 to 1.
Thus, while y2 is being integrated from 0 to 1/2, we integrate y1 from 1/2 to 1. No problem, 0<y2<y1<1 is satisfied here.
From 1/2 to 3/4 we have a different story. This is where we need to use a variable range of integration. y2 should be integrated from 1/2 to 3/4, but y1 should be integrated from y1 to 3/4. Alternatively, you can swap the order of integration and integrate y1 from 1/2 to 3/4 and integrate y2 from 1/2 to y1. You can prove that this order of integration swap works analytically for the general case, but here you only need a conceptual understanding like "yea, i can see how either way means the same thing". So that gives your second double integral (Note that in the image below I used the "alternate" method so that the order is consistent across all the integrals. But try it the reverse way just to convince yourself it's the same.
For the range 3/4 to 1, just like in the first case the inequality is always true, so we don't need a variable range of integration. only 0<y2<3/4 and 3/4<y1<1.
So, in closing, you end with the following:
http://www.khanacademy.org/ for ODE.
http://patrickjmt.com/ for multivariate calc because Khan doesn't cover it.
Buy yourself some cheap but highly reviewed textbooks from amazon and use the videos as your lectures and the problems in the books as practice.
http://www.wolframalpha.com/ to check your answers.
http://patrickjmt.com/ for multivariate calc because Khan doesn't cover it.
Buy yourself some cheap but highly reviewed textbooks from amazon and use the videos as your lectures and the problems in the books as practice.
http://www.wolframalpha.com/ to check your answers.
I really need help with the diagram for the following question (note / indicates division) Soh-Cah-Toa style (I know, I know):
2. The Son of Beast roller coaster at Kings Island in Cincinnati, Ohio is the tallest wooden roller coaster in the world. The highest point of the coaster is 66 m high. What is the angle of elevation, to the nearest degrees, to the top of the coaster from a point on the ground 72 m away?
3. The top of a 7 m ladder makes an angle of 15 degrees with the wall. How far away from the wall is the base of the ladder? Round to the nearest tenth.
I used Sin15=x/7 which became sin15(7)=x which is 1.8 m. Is that correct?
4. A 30 m high communication tower is located 50 m away from another tower which is 20 m high. Determine the angle of depression from the top of the taller tower to the top of the shorter tower. Round to the nearest degree.
I drew this as a diagram:
And used Tant=10/50 (because 10 m is the opposite to the angle, and 50 is adjacent). The problem is that doesn't give a full number, and doesn't feel right. Is it right?
2. The Son of Beast roller coaster at Kings Island in Cincinnati, Ohio is the tallest wooden roller coaster in the world. The highest point of the coaster is 66 m high. What is the angle of elevation, to the nearest degrees, to the top of the coaster from a point on the ground 72 m away?
3. The top of a 7 m ladder makes an angle of 15 degrees with the wall. How far away from the wall is the base of the ladder? Round to the nearest tenth.
I used Sin15=x/7 which became sin15(7)=x which is 1.8 m. Is that correct?
4. A 30 m high communication tower is located 50 m away from another tower which is 20 m high. Determine the angle of depression from the top of the taller tower to the top of the shorter tower. Round to the nearest degree.
I drew this as a diagram:
And used Tant=10/50 (because 10 m is the opposite to the angle, and 50 is adjacent). The problem is that doesn't give a full number, and doesn't feel right. Is it right?
cpp_is_king
Member
Takao said:I really need help with the diagram for the following question (note / indicates division) Soh-Cah-Toa style (I know, I know):
2. The Son of Beast roller coaster at Kings Island in Cincinnati, Ohio is the tallest wooden roller coaster in the world. The highest point of the coaster is 66 m high. What is the angle of elevation, to the nearest degrees, to the top of the coaster from a point on the ground 72 m away?
3. The top of a 7 m ladder makes an angle of 15 degrees with the wall. How far away from the wall is the base of the ladder? Round to the nearest tenth.
I used Sin15=x/7 which became sin15(7)=x which is 1.8 m. Is that correct?
4. A 30 m high communication tower is located 50 m away from another tower which is 20 m high. Determine the angle of depression from the top of the taller tower to the top of the shorter tower. Round to the nearest degree.
I drew this as a diagram:
And used Tant=10/50 (because 10 m is the opposite to the angle, and 50 is adjacent). The problem is that doesn't give a full number, and doesn't feel right. Is it right?
When you say it doesn't give a full number, do you mean the number is less than 1? Or just that it has a decimal? If you mean the first, then make sure you convert to degrees. If you mean the second, I don't see why that would be a problem, it's actually hard to construct problems to make sure numbers come out whole
- Status